Bit map and Bit-Slice indexing

What is indexing ?

Indexing is an interesting topic when it comes to databases. Indexing is a data structure which is used by database systems to improve the query performance. There are many indexing mechanisms, have been proposed throughout the evolution of database systems (eg :- value list, projection, B-tree, etc). Generally index is a pointer to the data (usually to the search key of data) and index file is less than the actual data file in terms of size. Indexing is more popular since it allows us to access data very fast. In this article we are talking about two indexing mechanisms called “bit map” and “bit slice”.

Bitmap indexing

Bitmap is a special kind of indexing mechanism where we create bit-vectors (called as bitmap) to represent the existence of a particular attribute value in a specific column. Let’s see the picture attached below. In that figure, in employee table gender column has two possible attribute values male and female. We can create two bitmaps related to each attribute values as shown in the diagram. “1” in bitmap, represents the existence of a value (male or female) while “0” represent the absence.

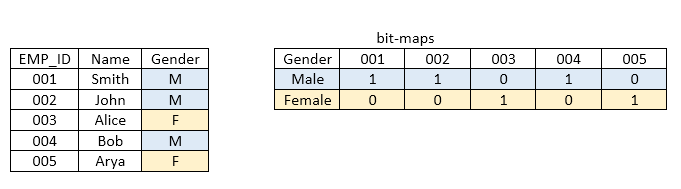
(EMP_ID is taken as the row identifier)

According to the above table we have two bitmaps for column “gender”. One bitmap is “male = 11010” and the other bitmap is “female = 00101”. But there is a drawback with bitmap indices, that is bit map index is suffering from the column cardinality. If the column cardinality is very high (if there are many number of distinct attribute values ), then the bitmap index file will be large in terms of size. Because there will be a single bitmap for each distinct attribute value (as in above diagram, one for male and the other for female, likewise). But on the other hand there are several amazing advantages as well.

Using only the bitmap index file (without referring to the actual data file), we can find results for queries which has bit wise operations like AND, OR , NOT, etc. And also aggregation functions like COUNT, can be efficiently performed with bitmaps. Further we use bitmap indexes like EBM (existence bitmap index) to enhance some query operations.

COUNT using bitmap index

/**
 *  B[] is a short int array overlaying a foundset bitmap
 *  shcount[] - short int array
 *	      -	declared to contain the number of bits in the entry subscript
 **/
 
count = 0.0;
for (int i=0; i < B.length; i++){
	count += shcount[B[i]];
}

shcount[] array is used to provide parallelism in calculating the COUNT on many bits at the same time.

Usage of EBM (Existence bitmap index)

EBM helps to identify, whether a raw is actually there in the data or not (whether it is deleted or not). If a row is deleted then the corresponding bit in EBM will set to 0. If a row is there in the data file then the corresponding bit will be 1. So we do not need to update every where in bitmap index when a row is deleted. It is enough to update EBM. And when we run any query, before taking the final result we should get the AND operation between bitmap of found set and EBM (reason is some bits in found set bitmap can corresponds to non-existence rows).

/**
  * Consider following example - getting NOT for raws that exist
  * B1[]  - bitmap of foundset
  * B2[]  = NOT(B1[])
  * EBM[] - existence bitmap
  *
  **/
  
for(int i=0; i< len(B1); i++){
  B2[i] = ~B1[i] & EBM[i];
}

Practical example

Let’s talk about several practical examples to see how bitmaps improve query performance. Consider the following employee table.

Employee Table

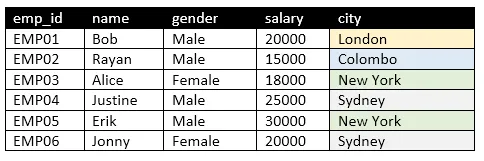
Lets create a bitmap index for column city. Since the column cardinality of city column is low (in this case it is 4), it is practical to create a bitmap index for the city column. We need to create 4 bitmaps for the column as follows (I used the emp_id as the raw identifier).

bitmap index for column city

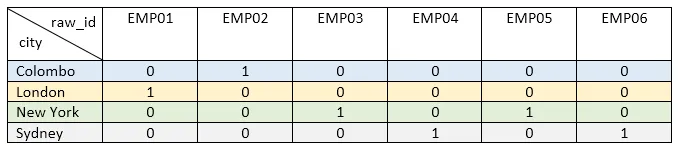
Now let’s answer to the following query,

/** 
  * Query to get employee names from the city "London" or "New York"
  **/
SELECT name FROM Employee WHERE city = "London" OR city = "New York";

Above query asks for the employees from London or New York. We can get the employees from London or New York city by getting “OR operation” between “London bitmap(100000)” and “New York bitmap (001010)”. So the result will be “101010”. In result we have 3 records found which satisfy the provided query. Same as above bitmaps can use to do bit-wise operations like AND, NOT.

Bit-slice indexing

Bit-slice index contains a set of bitmap indices. The smallest bit-slice index is a single bitmap index. Bit-slice index has solved the problem of high cardinality in bitmap indices. It is possible to create a bit-slice index to a numeric column (eg:- to salary column in Employee table above) and we normally create bit-slice indices on numeric columns. Bit-slice index is more popular because it is quite efficient in calculating aggregations.

Definition

For all i=0,…. N (N is number of bits in binary representation of a value) define a function D such that D(n,i) > 0 for some rows in the table ( in our case Employee table). Then define a bitmap B[i] on the table such that n th bit of bitmap B[i] = D(n,i). D(n,i) = 0 only if row contains a null value.

D(n,i) = 0 if row n has null value
D(n,0) = 1 if the 1st bit of row n is on
D(n,1) = 1 if the 2nd bit of row n is on
........................................
D(n,i) = 1 if the ith bit of row n is on

Simple idea — how to create a bit-slice index

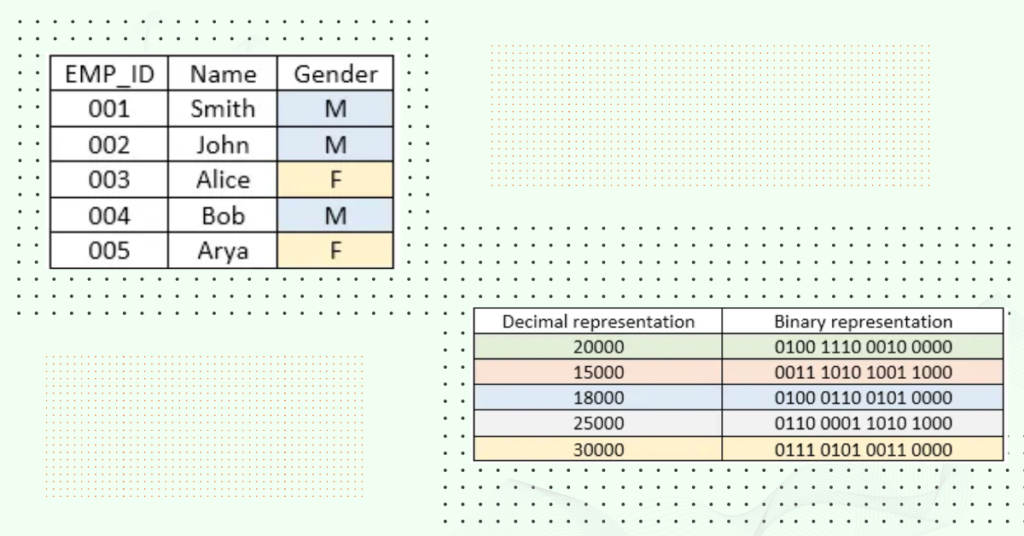
Convert the selected column values in to binary representation and slice them in to bitmaps (bit vectors) vertically as shown in following example. Following example shows the relevant bit-slice index for column salary in our example (in bitmap section). According to example we can represent values, range from 0 to 30000 using only 15 bitmaps.

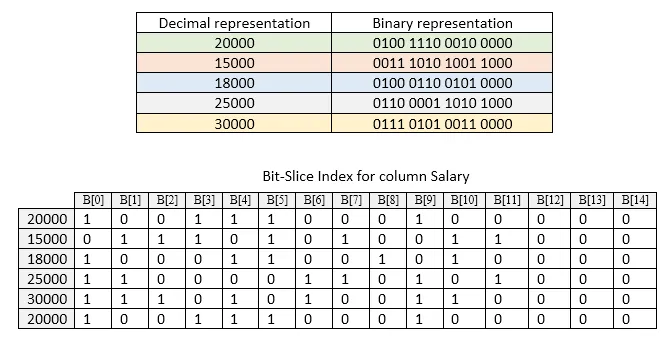
Bnn and Bn bitmap usage

Bnn is the bitmap for the not-null valued rows (contain 1 for not-null rows). And Bn is the bitmap for null valued rows (contain 1 for null valued rows). Bn can be derived by using EBM and Bnn bitmaps easily. Both of these are used to optimize algorithms.

SUM aggregation with bit-slice

/**
  * Assume we are given a bit-slice index B for specific column C
  * Bnn and Bn has usual meanings
  * Bf is bitmap for foundset
  * Here N means number of rows (or lenth of a bitmap in bitslice index)
  * COUNT is the same function used in bitmaps
**/

If (COUNT(Bf AND Bnn) == 0){
  return null;
}
sum = 0.0;
for(i = 0 to N){
  sum += 2^(i) * COUNT(B[i] AND Bf);
}
return sum;

RANGE predicate with bit-slice index

Consider the query “SELECT target-list FROM T WHERE C-range AND <condition>”. Here assume C is a column in Table T and <condition> is a general condition resulting in a found-set Bf. C-range represents, the range of column C values lies between two constants c1 and c2 .( or some range as follows C>c1 , C ≥ c1, C = c1, C < c2, C ≤ c2).

For a given found-set let’s define set of special bitmaps as follows,

special btimaps used in range algorithm

You can drop any evaluation condition in below algorithm if it not in your requirement. As an example if you only need to evaluate C ≥ c1 then you can drop steps that evaluate BLE or BLT.

range algorithm pseudo-code : source from reference[1]

Notes

In bitslice index it is necessary that different values should have same number of bits (N) in their binary representation. Variation in size of floating point numbers, could lead to an exceptionally large number of bit-slices when values differ by many orders of magnitude. But such situations are unlikely in business applications.

References

[1] O’Neil, Patrick, and Dallan Quass. “Improved query performance with variant indexes.” ACM Sigmod Record. Vol. 26. №2. ACM, 1997.

[2] https://en.wikipedia.org/wiki/Bitmap_index

Author

Chanaka Rathnayaka Avatar
Chanaka Rathnayaka